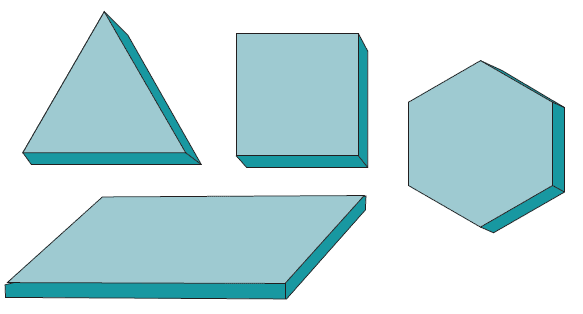
Pattern Blocks
Set of plastic, wood or cardboard shapes in the form of triangles, squares, parallelograms, hexagons, etc Examples
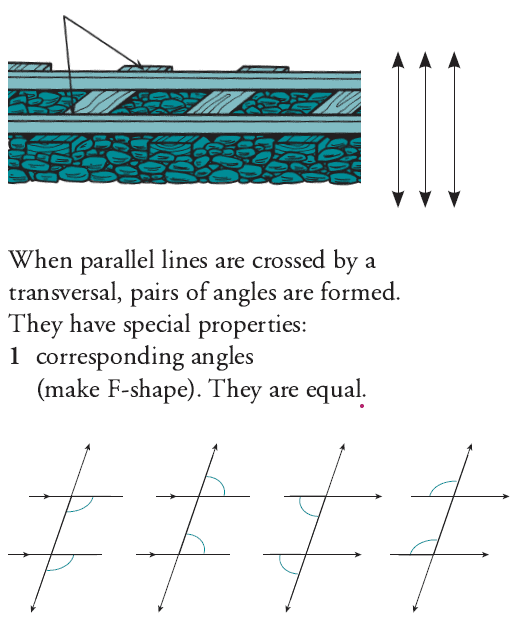
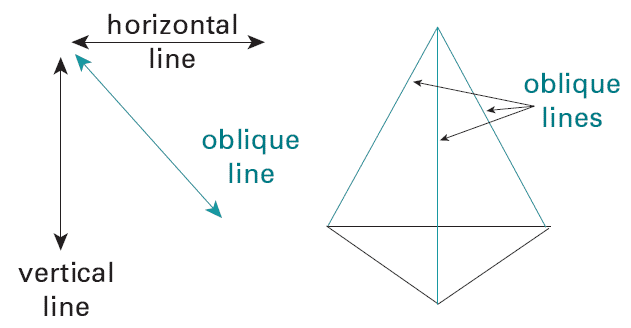
Parallel Lines
(Symbol: ∥ )Two or more lines that go in exactly the same direction. Parallel lines always remain the same distance apart. They never meet.
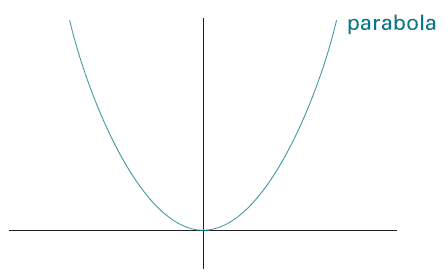
Parabola
A parabola is a conic section made by the intersection of a right circular cone and a plane. It can also be defined as a… Read More »Parabola
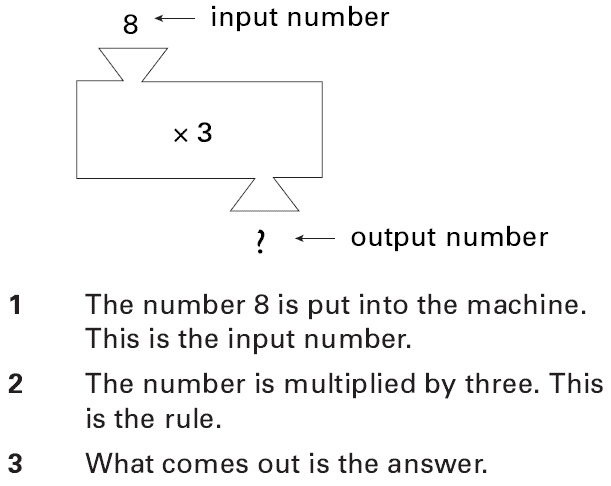
Number Machine
Number machines can carry out operations such as adddition, subtracition, multiplication and division. Calculators and computers are types of number machine. Example